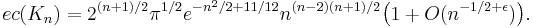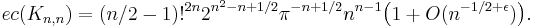Eulerian path

In graph theory, an Eulerian trail (or Eulerian path) is a trail in a graph which visits every edge exactly once. Similarly, an Eulerian circuit or Eulerian cycle is a Eulerian trail which starts and ends on the same vertex. They were first discussed by Leonhard Euler while solving the famous Seven Bridges of Königsberg problem in 1736. Mathematically the problem can be stated like this:

Given the graph on the right, is it possible to construct a path (or a cycle, i.e. a path starting and ending on the same vertex) which visits each edge exactly once?

Euler proved that a necessary condition for the existence of Eulerian circuits is that all vertices in the graph have an even degree, and stated without proof that connected graphs with all vertices of even degree have a Eulerian circuit. The first complete proof of this latter claim was published posthumously in 1873 by Carl Hierholzer.^[1]

The term Eulerian graph has two common meanings in graph theory. One meaning is a graph with a Eulerian circuit, and the other is a graph with every vertex of even degree. These definitions coincide for connected graphs.^[2]

For the existence of Eulerian trails it is necessary that no more than two vertices have an odd degree; this means the Königsberg graph is not Eulerian. If there are no vertices of odd degree, all Eulerian trails are circuits. If there are exactly two vertices of odd degree, all Eulerian trails start at one of them and end at the other. Sometimes a graph that has a Eulerian trail but not a Eulerian circuit is called semi-Eulerian.

1 Definition
2 Properties
3 Constructing Eulerian trails and circuits
- 3.1 Fleury's algorithm
- 3.2 Hierholzer's algorithm
4 Counting Eulerian circuits
- 4.1 Complexity issues
- 4.2 Special cases
5 Applications
6 See also
7 Notes
8 References
9 External links

Definition

An Eulerian trail,^[3] or Euler walk in an undirected graph is a path that uses each edge exactly once. If such a path exists, the graph is called traversable or semi-eulerian.^[4]

An Eulerian cycle,^[3] Eulerian circuit or Euler tour in an undirected graph is a cycle that uses each edge exactly once. If such a cycle exists, the graph is called unicursal.^[5] While such graphs are Eulerian graphs, not every Eulerian graph possesses a Eulerian cycle.

For directed graphs, "path" has to be replaced with directed path and "cycle" with directed cycle.

The definition and properties of Eulerian trails, cycles and graphs are valid for multigraphs as well.

An Eulerian orientation of an undirected graph G is an assignment of a direction to each edge of G such that, at each vertex v, the indegree of v equals the outdegree of v. Such an orientation exists for any undirected graph in which every vertex has even degree, and may be found by constructing an Euler tour in each connected component of G and then orienting the edges according to the tour.^[6] Every Eulerian orientation of a connected graph is a strong orientation, an orientation that makes the resulting directed graph strongly connected.

Properties

An undirected graph has an Eulerian cycle if and only if every vertex has even degree, and all of its vertices with nonzero degree belong to a single connected component.
An undirected graph can be decomposed into edge-disjoint cycles if and only if all of its vertices have even degree. So, a graph has an Eulerian cycle if and only if it can be decomposed into edge-disjoint cycles and its nonzero-degree vertices belong to a single connected component.
An undirected graph has an Eulerian trail if and only if at most two vertices have odd degree, and if all of its vertices with nonzero degree belong to a single connected component.
A directed graph has an Eulerian cycle if and only if every vertex has equal in degree and out degree, and all of its vertices with nonzero degree belong to a single strongly connected component. Equivalently, a directed graph has an Eulerian cycle if and only if it can be decomposed into edge-disjoint directed cycles and all of its vertices with nonzero degree belong to a single strongly connected component.
A directed graph has an Eulerian trail if and only if at most one vertex has (out-degree) − (in-degree) = 1, at most one vertex has (in-degree) − (out-degree) = 1, every other vertex has equal in-degree and out-degree, and all of its vertices with nonzero degree belong to a single connected component of the underlying undirected graph.

Constructing Eulerian trails and circuits

Fleury's algorithm

Fleury's algorithm is an elegant but inefficient algorithm which dates to 1883.^[7] Consider a graph known to have all edges in the same component and at most two vertices of odd degree. We start with a vertex of odd degree—if the graph has none, then start with any vertex. At each step we move across an edge whose deletion would not disconnect the graph, unless we have no choice, then we delete that edge. At the end of the algorithm there are no edges left, and the sequence of edges we moved across forms a Eulerian cycle if the graph has no vertices of odd degree; or a Eulerian trail if there are exactly two vertices of odd degree.

While the graph traversal in Fleury's algorithm is linear in the number of edges, i.e. O(|E|), we also need to factor in the complexity of detecting bridges. If we are to re-run Tarjan's linear time bridge finding algorithm after the removal of every edge, Fleury's algorithm will have a time complexity of O(|E²|) A dynamic bridge-finding algorithm of Thorup (2000) allows this to be improved to 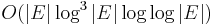$O(|E|\log^3|E|\log\log|E|)\,$ , but this is still significantly slower than alternative algorithms.

Hierholzer's algorithm

Hierholzer's 1873 paper provides a different method for finding Euler cycles that is more efficient than Fleury's algorithm:

Choose any starting vertex v, and follow a trail of edges from that vertex until returning to v. It is not possible to get stuck at any vertex other than v, because the even degree of all vertices ensures that, when the trail enters another vertex w there must be an unused edge leaving w. The tour formed in this way is a closed tour, but may not cover all the vertices and edges of the initial graph.
As long as there exists a vertex v that belongs to the current tour but that has adjacent edges not part of the tour, start another trail from v, following unused edges until returning to v, and join the tour formed in this way to the previous tour.

By using a data structure such as a doubly linked list to maintain the set of unused edges incident to each vertex, to maintain the list of vertices on the current tour that have unused edges, and to maintain the tour itself, the individual operations of the algorithm (finding unused edges exiting each vertex, finding a new starting vertex for a tour, and connecting two tours that share a vertex) may be performed in constant time each, so the overall algorithm takes linear time.^[8]

Counting Eulerian circuits

Complexity issues

The number of Eulerian circuits in digraphs can be calculated using the so-called BEST theorem, named after de Bruijn, van Aardenne-Ehrenfest, Smith and Tutte. The formula states that the number of Eulerian circuits in a digraph is the product of certain degree factorials and the number of rooted arborescences. The latter can be computed as a determinant, by the matrix tree theorem, giving a polynomial time algorithm.

BEST theorem is first stated in this form in a "note added in proof" to the Aardenne-Ehrenfest and de Bruijn paper (1951). The original proof was bijective and generalized the de Bruijn sequences. It is a variation on an earlier result by Smith and Tutte (1941).

Counting the number of Eulerian circuits on undirected graphs is much more difficult. This problem is known to be #P-complete.^[9] In a positive direction, a Markov chain Monte Carlo approach, via the Kotzig transformations (introduced by Anton Kotzig in 1968) is believed to give a sharp approximation for the number of Eulerian circuits in a graph.^[10]

Special cases

The asymptotic formula for the number of Eulerian circuits in the complete graphs was determined by McKay and Robinson (1995):^[11]

$ec(K_n) = 2^{(n%2B1)/2}\pi^{1/2} e^{-n^2/2%2B11/12} n^{(n-2)(n%2B1)/2} \bigl(1%2BO(n^{-1/2%2B\epsilon})\bigr).$

A similar formula was later obtained by M.I. Isaev (2009) for complete bipartite graphs:^[12]

$ec(K_{n,n}) = (n/2-1)!^{2n} 2^{n^2-n%2B1/2}\pi^{-n%2B1/2} n^{n-1} \bigl(1%2BO(n^{-1/2%2B\epsilon})\bigr).$

Applications

Eulerian trails are being used in bioinformatics to reconstruct the DNA sequence from its fragments.^[13]

Notes

^ N. L. Biggs, E. K. Lloyd and R. J. Wilson, Graph Theory 1736-1936, Clarendon Press, Oxford, 1976, 8-9, ISBN 0-19-853901-0.
^ C. L. Mallows, N. J. A. Sloane (1975). "Two-graphs, switching classes and Euler graphs are equal in number". SIAM J. Appl. Math. 28 (4): 876–880. doi:10.1137/0128070. JSTOR 2100368.
^ ^a ^b Some people reserve the terms path and cycle to mean non-self-intersecting path and cycle. A (potentially) self-intersecting path is known as a trail or an open walk; and a (potentially) self-intersecting cycle, a circuit or a closed walk. This ambiguity can be avoided by using the terms Eulerian trail and Eulerian circuit when self-intersection is allowed.
^ Jun-ichi Yamaguchi, Introduction of Graph Theory.
^ Schaum's outline of theory and problems of graph theory By V. K. Balakrishnan [1].
^ Schrijver, A. (1983), "Bounds on the number of Eulerian orientations", Combinatorica 3 (3-4): 375–380, doi:10.1007/BF02579193, MR 729790 .
^ Fleury, M. (1883), "Deux problèmes de Géométrie de situation" (in French), Journal de mathématiques élémentaires, 2nd ser. 2: 257–261, http://books.google.com/books?id=l-03AAAAMAAJ&pg=PA257 .
^ Fleischner, Herbert (1991), "X.1 Algorithms for Eulerian Trails", Eulerian Graphs and Related Topics: Part 1, Volume 2, Annals of Discrete Mathematics, 50, Elsevier, pp. X.1–13, ISBN 9780444891105 .
^ Brightwell and Winkler, "Note on Counting Eulerian Circuits", 2004.
^ Tetali, P.; Vempala, S. (2001). "Random Sampling of Euler Tours". Algorithmica 30: 376–385. http://www.springerlink.com/content/k5kbhmg4qkj7whcf/.
^ Brendan McKay and Robert W. Robinson, Asymptotic enumeration of eulerian circuits in the complete graph, Combinatorica, 10 (1995), no. 4, 367–377.
^ M.I. Isaev (2009). "Asymptotic number of Eulerian circuits in complete bipartite graphs" (in Russian). Proc. 52-nd MFTI Conference (Moscow): 111–114.
^ Pevzner, Pavel A.; Tang, Haixu; Waterman, Michael S. (2001). "A Eulerian trail approach to DNA fragment assembly". Proceedings of the National Academy of Sciences of the United States of America 98 (17): 9748–9753. Bibcode 2001PNAS...98.9748P. doi:10.1073/pnas.171285098. PMC 55524. PMID 11504945. http://www.pnas.org/content/98/17/9748.long.

References

Euler, L., "Solutio problematis ad geometriam situs pertinentis", Comment. Academiae Sci. I. Petropolitanae 8 (1736), 128-140.
Hierholzer, Carl (1873), "Ueber die Möglichkeit, einen Linienzug ohne Wiederholung und ohne Unterbrechung zu umfahren", Mathematische Annalen 6 (1): 30–32, doi:10.1007/BF01442866 .
Lucas, E., Récréations Mathématiques IV, Paris, 1921.
Fleury, "Deux problemes de geometrie de situation", Journal de mathematiques elementaires (1883), 257-261.
T. van Aardenne-Ehrenfest and N. G. de Bruijn, Circuits and trees in oriented linear graphs, Simon Stevin, 28 (1951), 203-217.
Thorup, Mikkel (2000), "Near-optimal fully-dynamic graph connectivity", Proc. 32nd ACM Symposium on Theory of Computing, pp. 343–350, doi:10.1145/335305.335345
W. T. Tutte and C. A. B. Smith, On Unicursal Paths in a Network of Degree 4. Amer. Math. Monthly, 48 (1941), 233-237.

External links

Discussion of early mentions of Fleury's algorithm